31. Ehrenfest Paradox 2: Does the length of a rotating circumference change?

  We looked at the Ehrenfest paradox last time. There are two issues in the Ehrenfest paradox. The first assumes a disc made up of an ideal rigid body, but when rotated at relativistic speed, it ruptures. The second is that the perimeter of a rotating body is different from its length when it is stationary.

In the last post I looked at the first issue, and this time I want to look at the second issue. For those who have not read the first part, I will briefly introduce this paradox. It is best to read the previous post. Below is a link to the first part.

The Ehrenfest paradox part I

Rotating disc and length contraction

  In relativity, objects that run very fast are said to shrink in length. So the official name of this is Lorentz - Fitzgerald Length contraction. It is not 'Einstein's length contraction'. This was born regardless of the theory of relativity. Before the theory of relativity was published, several people experimented to detect ether, but the experiment was negative. It is this length contraction hypothesis that was created to save the ether.

The rod of a straight line contracts simply, but what about the circular object? The perimeter must contract. But we cannot imagine it. It is obviously a disk, and if it is reduced, how is it reduced? Einstein also thought quite deeply. It is said that this problem led to thinking about general relativity.

If the rotating disc moves at a relativistic speed, it can be thought that the circumference of the disc is simply reduced because of the length contraction phenomenon. But we may think differently. If the circumference of the disc is reduced, there is an empty space between them. If you think that you fill the empty space with the same ruler, you might think that the length is increased. It seems like a lot of different people's thoughts.

Whatever the case, many people have tried to solve the problem of turning disks using length contractions, but there is no plausible solution yet. 

The existence that runs and does not exist

  Many scholars have studied this problem. However, they did not find the right solution and reached today's situation. In fact, this is natural. With length contractions, no matter how hard they try to find a solution, it cannot be solved. Discarding the length contraction can solve this problem. Now let's solve this problem.

Spaceship B is moving in space A. Spaceship B is  definitely moving and empty space A is not moving. So it is the spaceship B that has relativistic effects, not A at all. Since A is just space, there is no reason to have a relativistic effect. This is obvious.

Now there is another spaceship. What is moving in the picture above is spaceship B and C, never empty space A.  If a length change occurs, it definitely happens only on spaceship B and C, and empty space A does not have any relativistic change or length change.

Let's look at the picture above. Figure (1) is a non-relativistic view, and Figure (2) is a relativistic view. Let's take a look at picture (1) first. What is moving in this picture is the atoms a and b. The empty space i between them is never moving. Therefore, there is no reason for void space i to have a relativistic length change.

Next, let's look at the picture (2). Figure (2) is a relativistic view. If an object moves at relativistic speed, the length of the object does not decrease, but rather expands. (I would appreciate it if you would listen to my opinion, because it is impossible to solve the Ehrenfest paradox with length contraction.) I will start the logic under the assumption that the length expansion is correct.

If so, the orbitals of atom a' and atom b' in picture (2) will be stretched to prevent disassembly of the disks. And here it is important to keep in mind that the empty space i' has absolutely no relativistic effect.

The difference between Bell's spaceship paradox and Ehrenfest paradox

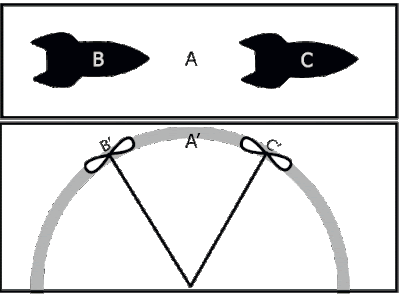
There are two pictures above. The upper part is the empty spaces with the first two spaceships, and the lower part is empty space and the disk of Ehrensest. The same principle applies. A and A 'are both empty spaces and do not have relativistic effects. There is reason to emphasize this over and over again.

Choosing the two most difficult paradoxes of relativity is probably the paradox of Bell's spacecraft paradox and of Ehrenfest paradox. However, Bell's spacespace paradox is surprisingly easy to solve  when the theory of length expansion is introduced, Bell's spaceship paradox is not a paradox at all, but a simple common sense.

However, Ehrenfest's paradox has an important difference from Bell's paradox. Below is it.

   The above picture shows Bell's spaceship paradox, and below is the Ehrenfest paradox. Bell's paradox assumed that the distance between the two spaces was constant, and that Ehrenfest's paradox assumed that the radius of the disk was constant. The premises between the two paradoxes are different.

   In the Ehrenfest paradox, we assume that the radius of the disk is constant, which is fair. Of course centrifugal force will work, but if centrifugal force and centripetal force are the same, there is no problem. In fact, such disks are found in black holes. Now let's focus on the picture below.

Is there a difference between the length of the arc between B 'and C' and the length of the arc between B 'and C' when it is stationary? There is no difference. A' in the middle does not move, so there is no change in length. Since the radius is constant and B' and C' are at the end of the radius, there is no reason to change the length of arc B'C' if it is always in the same position. There will be a myriad of atoms between B' and C', and when treating them as dots, the length of the arc is always constant. Even treating them as orbitals only increases the overlap of the orbitals on the spot. Therefore, no matter how fast the disk moves, the length of the disk is not changed.

So now two issues are resolved. I told you that the disk is not ruptured in the previous post, and in this post I have told you that the length of the disk does not change. If there is a contradiction in my logic development, please criticize me a lot. Thank you for reading the long story.

Length Expansion(Amazon books)