27. K Calculus (#3/6): Relationship between Relativistic Doppler Effect and Relativistic Length





Let's take a look at the relationship between relativistic Doppler effects and relativistic lengths. Before that, there are a few things to look at.

Some basic assumptions


Figure 1. Constant speed


Figure 1 (a) shows the propagation of light. At this time, the interval of the propagation of light with respect to the unit time is always constant. Anyone can see it. It does not depend on the speed of the observer. This is called the principle of invariant of light speed. And (b) shows an object moving at a constant speed. It is reasonable to state this way.


Figure 2. Light path inside a light clock moving at a constant speed

   So if an object is slower than light but moves at a constant speed, it will be drawn as shown in Figure 2 above. The light clock oscillating vertically moves to the right at a constant speed. If the light path is shown in detail, it will appear as shown below.

Figure 3. A light clock oscillating in a vertical position

In this case, when a relative stationary observer sees this, the point where the light departs and the point where it arrives are different. There are also a reflection-points between the starting and end points. Since the principle of invariant light speed and the isotropy of the propagation of light are established, it does not matter if the light clock tilts a little.


Figure 4. A light clock moving in a tilted state

As shown in Figure 5 below, it may be more inclined.

Figure 5. A light clock oscillating parallel to the direction of travel


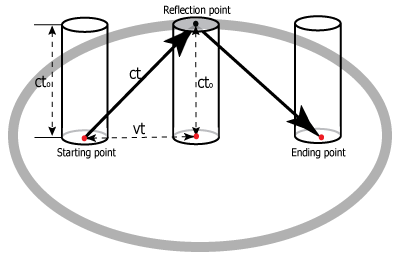
In order to establish the principle of invariant light speed, the starting point and the end point should be the two focus points of the ellipse, and all the reflection-points should be on the ellipse. Drawing this picture is as follows.


Figure 6. The principle of invariant light speed and ellipse

The following article links to this article, so it is helpful to read this post now after reading the following first.




The meaning of k here is the ratio of Alice's time to the time of John. In the figure above, this ratio is 1.5.

Meaning of k

Relativistic Doppler effect



We looked at the k factor in the last post. Now, let's create a table to better understand the properties of k. When the proper wavelength λo is set to 1, it shows the change of the wavelength depending on the speed. The speed is expressed as β (= v / c). The speed was changed by 0.1 unit.

Table 1. Change of wavelength according to the speed when proper wavelength is set to 1



Let's look at the second column in Table 1. It shows the wavelength when the light source approaches, and as the speed increases, the wavelength becomes shorter. Therefore, it is natural that the frequency is high. This is shown in the figure below. (I painted the light here in a sphere-shape, but it's not really a sphere. I have to draw with an ellipse, but I painted it in a circle to make it easier to understand.)
Figure 7. Change in wavelength when the light source approaches



The wavelength at which the light source moves away from me is shown in Figure 8 below. This is shown in the third column from the left in Table 1. The faster the speed, the greater the wavelength will be. This is also shown in Table 1.

Figure 8. Change in wavelength when the light source is moving away

And the content of the fourth column is the wavelength when the light source crosses in front of me. This is exactly the form of time delay and length expansion. So let's look at the table now. What is the average of the wavelengths when the light source is distant and the wavelengths when they are approaching? The average is shown in the rightmost red box. Table 1 will be rewritten below.


Table 1. Change of wavelength according to the speed when proper wavelength is set to 1



The average of the two wavelengths (the wavelength of the light coming away and the wavelength approaching) is exactly the same as the wavelength due to the transverse Doppler effect. In fact, it is a very natural story. Let's take a look at this equation.






What does this mean? We can look at relativistic length here using the Doppler effect.


Figure 9. The wavelength at the time of going back and the wavelength of light at the return, and k



Figure 9 above shows the same situation as Figure 5. The light is the process of returning to the reflex point. So when it goes away, the wavelength becomes longer by k times, and when it approaches, the wavelength becomes shorter by k-1 times.


Figure 5. A light clock oscillating parallel to the direction of travel


Figure 10 below shows all these situations at once. The left shows the relative stationary state, and the right shows the movement state.


Figure 10. Relationship between light and wavelength oscillating in various directions


Light that oscillates vertically up and down when stopped, and diagonal when running. When the object is moving fast, the light that oscillates vertically (red) increases its unit time and unit path size by γ times. The time was also increased, the time delay occurred, the wavelength became longer and the length expanded. And when the light goes up, it increases by K times, and when it comes, it decreases by k-1 times. Here, let us recall the definition of an ellipse. The definition of an ellipse is as follows.


"An ellipse is a curve in a plane surrounding two focal points such that the sum of the distances to the two focal points is constant for every point on the curve."


Remembering the definition of an ellipse, let's take a closer look.

Figure 11. Definition of ellipse


According to the definition of an ellipse, (AO) = (F1C) and (BO) = (F2C). (F1C) + (F2C) is the path of the vertically oscillating light clock, (AO) + (BO) is the path of a light clock that oscillates in parallel. They have the same length of path by the definition of an ellipse. The eccentricity is β. The eccentricity of the circle is 0, and the smaller the eccentricity, the closer to the circle. Now let's check this out in the ellipses. It is shown in Figure 12 below.


Figure 12. Definition of ellipse and path of light

In Figure 12 above, the sum of the red path and the sum of the blue path are the same in length by the definition of the ellipse. This is obvious. And the red path is the path of the light in the vertical state, and the blue path is the path of the light in the horizontal state. Both are equal in length by the definition of an ellipse. Compare Figure 12 and Figure 10. You can see that the relationship below is certain.




It can be seen that the above equation is also established by the definition of the ellipse. It is a very natural story. This must be done by the definition of the ellipse, and even if we consider the principle of invariant light speed, it must be.


Figure 10. Relationship between light and wavelength oscillating in various directions

Relativistic length


  When we define the length, we define the distance the light travels. And Hermann Bondi, in his book 'Relativity and Common Sense', says:


This result, as has been

This result, as has been stressed before, is indeed obvious once it is agreed that distance measurements should be made by radar methods. For then one measures a time, half the time between the emission and the return of the radar pulse, in order to determine the distance of the target. 

This is commonly referred to as 'radar length' or 'asynchronous length'. This is a legitimate way to measure length and is logical. So we can also use it to measure the length of a running object. Dividing the total path length by which light travels is divided by 2, which is the length of time the object moves.

 It is also commonly used when architects measure the size of a building when it detects a fisherman, measures the distance from the earth to the moon, and so on. Please do not deny this.

Figure 12. Twice the length of light clock


We can think of these objects simply as light-clocks, and those light-clocks must satisfy the elliptical theorem. So the light must start at the focus of the ellipse and be reflected at the reflection-point, the boundary of the ellipse, and reach the end point, which is the focus of the ellipse.

Figure 5. A light clock oscillating parallel to the direction of travel

If so, the sum of these paths will be twice the length, which is equivalent to the definition of the ellipse, so its length is the same in either direction. In particular, when it is parallel to the object's direction, its wavelength is k(when it goes away) and k-1(when it comes). This is exactly the same as the relativistic Doppler effect.

 We must now think deeply about the meaning of these statements. The time has come to think about just relativistic length.
Figure 14. Relatively stationary light clock


An observer who is relatively stationary watches a light clock. The observer can think of it as 'two seconds' when the light travels on two sides of the cylinder as shown in Figure 14 above. Keep this shape and move to the right as shown in Fig. 15 below. This is well known.



Figure 15. Moving vertical vibration light clock

In Figure 15 above, the time dilation can be easily derived. However, even if the light clock is tilted slightly, we cannot induce a time delay. Furthermore, it is impossible to induce length contraction in this picture. In Figure 15, it is a paradox that cannot induce length contraction. But there are more difficult challenges than this. Relative length cannot be obtained when the direction of the light is parallel to the direction of the light clock. Please try it once. This is not possible with the current theory of relativity.


But if we use what we have seen so far, this problem is solved at once. Now let's look at the process.

Figure 16. Light clock oscillating parallel to the direction of motion
When oscillating in parallel in any direction, it is the sum of k and k-1. If so, this is all settled. The following expression explains:

That is, in Figure 17, the length of the red path means exactly 2 wavelengths. We have seen enough of the above equation in Table 1 above.

     1. Table 1
    2. Elliptical Theorem
    3. The principle of invariant light speed
    4. Isotropy of light propagation
    5. Relativistic Doppler Effect

 These above previously mentioned five things guarantee it. Replace the wavelength with the length as shown below.

In other words, the red path in Figure 17 tells you exactly the 'length expansion'. So, if you write down a key expression about length, it is as follows.

If you mark this as 'L', which means length, it is as follows.

The length is the expansion. There is no contraction in length here. The same is true for Table 1. Length contraction cannot be found anywhere. If you cannot believe it, try it yourself. Length contraction is never induced. Looking vertically or parallel to light, the only reasonable length is the length expansion.


The appearance of light propagation and k


Now, let's not think of the light clock, but think about the light going straight. When the light moves away from me, it will move away as shown below. And its size is k.

Figure 18. Size of the wavelength when the light source is moving away

And when the light comes, the wavelength is as follows.
Figure 19. Size of the wavelength when the light source approaches

 k is the progressive light and k-1 is the approaching light, so it is perfectly one cycle. And this corresponds to twice the length. Now let's look at the whole picture of light propagation.

Figure 20. Doppler effect and wavelength size
When the observer is on the left, the full view of the light propagation will look like Figure 20. Figure 20 shows an ellipse, though it is a light propagation. This is how real light is propagated. It can be expressed more clearly if it is expressed in the three-dimensional (two-dimensional space + one-dimensional) space-time diagram.

 When the object moves away, it will come away forming a wavelength with k, k, k, and when approaching it will come up forming a wavelength with k-1, k-1, k-1. This creates red shifts and blue shifts. The following figure shows a light clock that oscillates parallel to the direction of the object.

Figure 21. Oscillating light clock and partial Doppler effect

 In Figure 20, k and k-1 are continuous, but in the case of a light clock, k and k-1 alternate. Despite these differences, what they have in common is that their speed of light is all the same.

 As we have seen, we have seen how the fundamental rate of relativity k is linked to its length. It was able to confirm that it was not length contraction but length expansion. When discussing the detailed mechanism of light propagation or light path, there is no place for length contraction. The following expression tells it.



Thank you for reading this long story.
















Comments

Post a Comment

Popular posts from this blog

06 Muon Paradox

Image
   Today, I would like to talk about the muon paradox. There are several subatomic particles that are smaller than atoms, such as a μ-meson. It is called a μ-meson, but it is abbreviated to muon. The lifetime of this muon is fixed. The proper lifetime of this particle is 2.2 μsec. It only survives for a very short moment, and then  it collapses into other particles. Cosmic-rays are constantly coming out of space due to the explosion of stars in the universe or the nuclear fusion reaction of the sun. At this time, the cosmic-ray and the earth's atmosphere react to create a muon. Muon's speed is near the speed of light when it falls to Earth. It drops at a rate of about 0.998c. However, even if it falls so fast, it cannot reach the ground because its life is short. If the muon has a lifetime of 2.2 μ sec and a speed of 0.998 c, the muon can run about 650 m from the point where it was created. The point where the usual muon occurs is about 10km above sea le...
Read more

10 Rotating disc of black hole and Ehrenfest's paradox

Image
  Black holes are unusual in many ways. Thet have also has a spinning disc, a jet, a Schwartzchild radius, a horizon of events and singularities. But there is one thing that can not be explained in modern science or the theory of relativity. It is the rotating disc of a black hole. Black hole and Ehrenfest paradox   The speed at which materials rotate in the rotating disk of a black hole is almost as close as the speed of light. If so, all the materials must be decomposed and discarded by the Lorentz contraction. However, the rotating disk of a black hole certainly exists. It is definitely a contradiction. In fact, these are linked to the famous paradox of the Ehrenfest paradox. [1] Today, we will look at the Ehrenfest paradox. Fig. 1 Paul Ehrenfest Personally, I think Erlenpest paradox is the best of relativity's paradoxes. Other paradoxes seem to be a little simpler than this paradox. The list of people who studied this paradox is very extensive. Ein...
Read more

31. Ehrenfest Paradox 2: Does the length of a rotating circumference change?

Image
  We looked at the Ehrenfest paradox last time. There are two issues in the Ehrenfest paradox. The first assumes a disc made up of an ideal rigid body, but when rotated at relativistic speed, it ruptures. The second is that the perimeter of a rotating body is different from its length when it is stationary. In the last post I looked at the first issue, and this time I want to look at the second issue. For those who have not read the first part, I will briefly introduce this paradox. It is best to read the previous post. Below is a link to the first part. The Ehrenfest paradox part I Rotating disc and length contraction   In relativity, objects that run very fast are said to shrink in length. So the official name of this is Lorentz - Fitzgerald Length contraction. It is not 'Einstein's length contraction'. This was born regardless of the theory of relativity. Before the theory of relativity was published, several people experimented to detect ether, but the...
Read more