26. K Calculus (#2/6): Relativistic Doppler Effect
Last time we tried to derive the fundamental ratio k of relativity, and we looked at twin paradoxes based on that. This time, we will briefly review the theory of relativity (velocity addition), time dilation and the relativistic Doppler effect. To understand this article, it is recommended that you read the previous article first.
The k in this article is not particularly mysterious, but rather the ratio of John and Ellis' time. When John sends a signal every 4 seconds, James receives it every 4 seconds, but Alice receives a signal every 6 seconds. So it becomes (4: 6), which can be expressed as (1: 1.5). At this time, k is 1.5.
We know that in the theory of relativity, the speed of any object does not exceed the speed of light. First, let's take a look at how K Calculus really does.
Velocity-addition formula
Based on john, Alice is rapidly moving away, and James is quickly moving away from Alice. So let's calculate how fast James is about John. Last time we looked at K. If the speed of light is set to 1, the equation is as follows.
 |
| Hermann Bondi's notation |
 |
| Common notation |
We knew how to get the speed of the other party through the ratio of time to each other. The equation is shown below. If you know only K value, you can find the speed of the other party.
Now, based on this, let's look at whether the composite speed exceeds the speed of light when we add two speeds.
 |
| Derivation of relativistic velocity-addition formula of Hermann Bondi |
(1) is the ratio k when john observes Alice,
(2) is the ratio of Alice observing James. And
(3) is the rate of synthesis when john observes James.
(4) is calculated by adding a formula (1) and an equation (2) to the formula (3).
As a result of the calculations, we know the speed of the composite. No matter how fast you put the expression in (4), you can see that it does not exceed 1.
Relativistic Doppler effect
There are two important differences between the classical Doppler effect and the relativistic Doppler effect. First, the classic Doppler effect is calculated differently both when the sound source moves and when the observer moves. But relativistic Doppler effects have nothing to do with whether the light source is moving or the observer is exercising. (1) Relativistic Doppler effects are related only to the relative motion of the two observers. Sometimes, people say that sound and light are the same as waves. This difference is the crucial difference.
And (2) one difference is that no transverse Doppler effect is found in the classical Doppler effect (the transverse Doppler effect is when the object crosses vertically in front of the observer). This is the crucial difference. Below is a graph of the difference.
 |
| Transverse Doppler effect: Variation of frequency depending on speed. Robert Resnick, David Halliday, Concepts in Relativity and Early Quantum Theory, 75p |
The horizontal axis is the moving speed of the object, and the vertical axis is the difference between the proper frequency and the observed frequency. As the speed of the object increases and the relative effect increases, the value increases steeply. So this is proven both theoretically and experimentally. Let's look at the relationship between the relativistic Doppler effect and k.
We have previously seen a brief look at the transverse Doppler effect. The equation is shown below. The equation for this relativistic Doppler effect is widely known.
If you look at these equations, they are all in frequency. (Speed of light = frequency × wavelength). Let's modify this equation to the form of wavelength. The frequency is a reciprocal of time, and since the dimension is T-1, it is not intuitive to touch. So let's change to the unit of length we are familiar with. Then all relativistic Doppler effects become L-dimensional and intuitive to understand easily.
The speed of light is constant regardless of the light source. So, no matter how different observers measure, their value should not change. So the above equation must always be established. If so, we can write down as follows.
In the above equation, if only red is drawn, it becomes like the following expression.
This is the relativistic Doppler effect as a representation of the wavelength. So let's write down the frequency and wavelength.
In the above figure, the equations in the blue boxes show the relativistic Doppler effect in terms of wavelength. These equations are not well known because they are the opposite of the Lorenz contraction formula. The expression in red is an expression for the transverse Doppler effect among relativistic Doppler effects. Since the dimension of the wavelength is the length, you should apply the relativistic length change to the wavelength. The results are shown in the form of length expansion rather than length contraction.
Length contraction is difficult to become truth. Forcing the length contraction equation to show the Doppler effect, the principle of invariant of light speed is destroyed. If a theory destroys the constancy of the speed of light, it is not a theory of relativity. When we calculate the equation for the Doppler effect, we have kept the principle thoroughly. As a result, the length expansion was induced immediately. Please refer to the contents of the previous post for this content.
Let's now write down these equations and the K value. If you do so, it looks like this:
The expression of the relativistic Doppler effect in terms of wavelength and the k value are the same.
Relationship between Doppler effect and K
In the figure below, the value of the Doppler effect, expressed in terms of wavelength, and the K value match (red box). To see what this means, we'll show it with a graph.
We can express it simply as shown below.
Separating: λ = K λo
Approaching: λ = K-1 λo
Transverse: λ = γ λo
Approaching: λ = K-1 λo
Transverse: λ = γ λo
The k value is the value for the Doppler effect. The relativistic Doppler effect does not matter whether John observes Alice or Alice observes John. If the relative speeds of the two systems are the same, the magnitude of the Doppler effect is the same. In the above picture, from the viewpoint of the observer P, it is k when it goes away, k-1(it is inverse because the time is reversed) when it approaches, and Lorentz parameter γ when it goes vertically. Because wavelength is length dimension, length becomes like this.
In other words, we know the relativistic effect of wavelength. Therefore, we have come to know the length when an object comes, the length when it goes away, and the length when it goes across. No matter how much we focus on here, the Lorenz-Fitzgerald length contraction does not exist.
(T2 / T1) is equivalent to knowing the unit time or unit length of the other party in terms of my unit. The meaning of this is clearer when it is interpreted through the picture below.
Figure (a) shows T1 as the physical quantity of the stationary system observer. This is equal to the magnitude of the transverse Doppler effect, or time dilation. Let's take a closer look at this. The path of the object marked in red in (a) is the same as the path of the red light shown in (b). However, the path of this red object is the same as the round trip time of the light clock. This is intuitively drawn in (c).
Figure (b), the moving time of the object (red) and the light travel time (dot blue) are the same. Therefore, comparing this with the time of the relative stationary observer leads to a relative time ratio. So let's get (T2 / T1).
Derivation of the transverse Doppler effect
Now, we will derive the transverse Doppler effect λ = γ λo. This equation is derived simply from the frequency version of the transverse Doppler effect. However, let's start from the beginning using the K Calculus method.
What we want is (T2 / T1). If you look at T1 first, T1 is simply kT. Then T2 is shown below. (If you have any questions, please leave a comment.)
(T2 / T1) is equivalent to knowing the unit time or unit length of the other party in terms of my unit. The meaning of this is clearer when it is interpreted through the picture below.
Figure (a) shows T1 as the physical quantity of the stationary system observer. This is equal to the magnitude of the transverse Doppler effect, or time dilation. Let's take a closer look at this. The path of the object marked in red in (a) is the same as the path of the red light shown in (b). However, the path of this red object is the same as the round trip time of the light clock. This is intuitively drawn in (c).
Figure (b), the moving time of the object (red) and the light travel time (dot blue) are the same. Therefore, comparing this with the time of the relative stationary observer leads to a relative time ratio. So let's get (T2 / T1).
So the ratio of (T2 / T1) is γ. This is the time dilation. This is the same as the transverse Doppler effect, as we have seen above. The transverse Doppler effect is usually expressed as a frequency, but this is the same as the time dilation.
All of the above equations express the transverse Doppler effect. (5) is an equation for the transverse Doppler effect that is commonly known, and (6) is simply a frequency interpreted as a wavelength rather than a frequency, and (7) the lowering of the frequency means that the time dilates, (8) The longer the wavelength is, the sooner the length will expand.
What k and k-1 mean is understandable to some extent now. k is the wavelength of light when it is away from me, and k-1 is the wavelength of light when it comes to me. And you can see that γ is the wavelength of light when you cross the front of me. However, there are important things related to these k values. Next time, let's look at this in relation to relativistic length and elliptic theorem. Thank you.





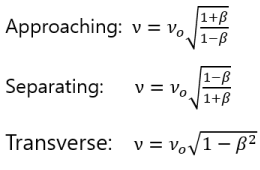















Comments
Post a Comment