11 Relativity theory and symmetry



  Symmetry is beautiful and intuitive. Symmetry is efficient and economical. And symmetry is an important principle that exists in the base of nature. And symmetry in relativity is very important.

 When we often say symmetry, we think of the symmetry of a figure. We call it line-symmetry or point-symmetry, where the left and right are the same or symmetric about a certain point. A Human is line-symmetrical, and the virus of the regular icosahedron is point-symmetrical.
Fig. 1 Line-symmetric human body
Fig 2. Point-symmetric virus

But symmetry in science is a bit different from the symmetry of geometry. It is called symmetry, even though it is not symmetrical about any line or point and does not change for a particular action. This is what we call symmetry when we have made a certain action on a physical object and it has not changed. The symmetry is summarized as follows.

Types of symmetry


In relativity, symmetry and conservation are also very important. The principle of relativity, the first principle of relativity, says that all inertial systems are symmetrical to each other. And the second principle, the constancy of the speed of light, states that the speed of light is preserved in all inertial systems. Symmetry and preservation are essentially the same story.

Suppose an object has a momentum of 100p. Then, when the observer moves 10 meters, he still has a momentum of 100p. Then the momentum is preserved for the space movement. Spacetime symmetry is the same. For a relatively stationary observer, the speed of light is c. And the other person observes this light while moving at 0.8c. The speed of light is still c. Then we say that 'the speed of light is symmetrical about spacetime movement'.

Energy and momentum are invariant to time and space, but various invariants such as speed of light, 4D-speed, and 4D-momentum in relativity are invariant to spacetime change. So, it is said that it is the Lorentz transformation that moves thing in spacetime. 
So we can say that the speed of light is invariant to the Lorentz transformation. This is easily referred to as the "invariance of the speed of light" or "the constancy of the speed of light".

Today, I will concentrate on the symmetry of relativity. I cannot help but talk about symmetry while talking about relativity, and I cannot help talking about space-time symmetry by talking about symmetry. In general relativity, which deals with non-inertial systems, this is sometimes broken, but it must be observed in special relativity theories that deal with inertial systems.


Evidence of space-time symmetry


  In fact, the theory of relativity does not need a basis for symmetry in time and space because it is so natural. Lorentz and Einstein designed it to be symmetrical, but it is abnormal that it is not symmetrical. The Lorentz transformations are precisely equally mixed in time and space. So the basic stage of relativity is not time, space, but 'spacetime'. So transforming in the Lorentz transformation is the same as changing it in spacetime.

 In inertial systems, the words 'invariant for Lorentz transformation' and 'symmetry in space and time' are identical. If there is no symmetry about spacetime, it cannot be said that it is invariant to the Lorentz transformation, which means that the Lorentz transformation is not necessary. Special relativity, which does not hold this, is no longer a theory of relativity.

 The first evidence is the Lorentz transformation. The Lorentz transformations in which objects travel in arbitrary directions are complex, but the transformations that proceed only in the + x axis are straightforward. It is as follows.

Lorentz transformation

 Now, the above four expressions do not match the dimensions. So, to match the dimension, let's multiply both sides of the expression by c in the first expression above. Then it looks like this:

Match the dimensions of four components
Let ct=xo, ct'=xo', β=v/c, x=x1, y=x2, z=x3. Then, the above two expressions are as follows.

Totally equal and symmetric

 In this way, the two expressions are completely equal. They are completely mixed and completely symmetrical. There is no difference between these two expressions. So we call this 'spacetime symmetry'.
The second proof of spacetime symmetry is the Minkowski spacetime diagram. It is well known that the 4-dimensional Minkowski spacetime diagram is used to represent the events of relativity. Since the 4th dimension cannot be displayed on the plane, if you reduce space to one dimension, Minkowski's spacetime diagram is as follows. Only one quadrant is shown.

Cartesian coordinate system, symmetrical about the speed of light c

Oblique coordinate system, symmetrical about the speed of light c

In order to show a quantitative relationship, a hyperbola is introduced as shown below.
Hyperbola based on invariants

Looking at the three graphs above, all are exactly symmetrical about the world line of light speed c. Since the equation above is symmetric, the graph must also be symmetrical. If you look at this space time diagram, you can quickly see whether it is symmetric or not symmetrical.


Destruction of symmetry


  Schröder expressed time dilation and length contraction in the spacetime diagram. (Ulrich E. Schröder, "Special Relativity", World Scientific, Singapore, 1990, p. 99.) Let's take a look at his expression. The Cartesian coordinate system is a representation of a proper physical quantity of an observer, and the oblique coordinate system is a transformed physical quantity of a moving system. In the following figure, the left shows the time dilation and the right shows the length contraction.

Time dilation and length contraction as shown by Schröder's method

In the left figure, the vertical axis represents time. OA <OB. Schröder says this is a representation of the time dilation. This is of course justified. Schröder, however, suddenly changes all of the rules used in time dilation without reason. So he claims to be OQ <OP. If the original rule is applied, it must be OR>OP. And this is called 'length contraction'. As a result, time dilation and length contraction became asymmetrical with each other in the spacetime diagram.

 Is there any difference between the rules for representing time and the rules for representing space in spacetime diagram? The method used by Schröder is simply not the other way around, it is actually the opposite. Those who support length contraction explain the muon paradox in terms of the muon. There is no one in the world that can ride on a muon and observe the earth. Only in thought. Changing the rules here is no different from asserting that everything is solved by observing Earth on board a muon. This is expressed in an analogy as follows.

First of all, I apologize to the model. One side is normal and the other side is abnormal, so it is not symmetrical. I do not know if anyone would like this more personally. One can embrace the asymmetry of the other, but the theory of relativity is impossible. The change in length must be exactly symmetrical with the time delay. It is not a length contraction but a length expansion. That way it becomes symmetrical.


If we superimpose the left figure and the right figure, it is exactly symmetrical about the light speed c. It coincides well with the basic spirit of the spacetime diagram, and it also matches well with the basic philosophy of relativity and the Lorentz transformations. If you compare this to a picture, it will look like this.



A harsh price for the destruction of space-time symmetry


  As I said at the beginning, symmetry is beautiful, but very powerful. On the other hand, the result of asymmetry in relativity is scary. As a result of asymmetry, it makes the current theory of relativity to be an incorrect theory of relativity. It will destroy the essential identity of relativity.

In a nutshell, the theory of relativity has a design that makes space-time symmetrical. But what about the buildings built by the plan? The current theory of relativity completely ignores space-time symmetry. The building was not built according to the plan. The building collapses without surviving the tiny earthquake. Let's look at the scene from now on.


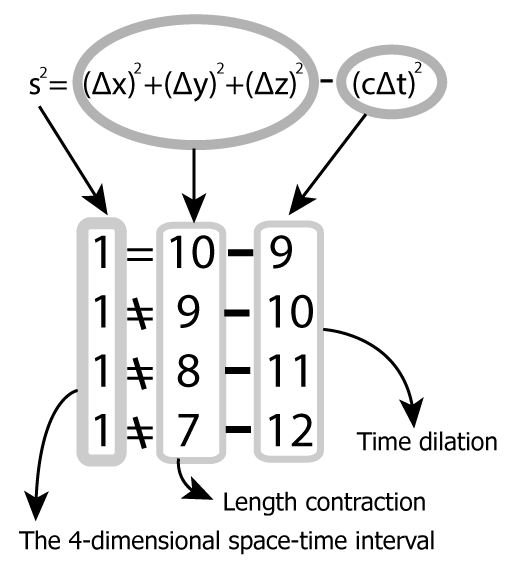
The first is the collapse of the constancy of the speed of light. In the case of asymmetry such as 'time dilation - length contraction', there is almost no indication at low speed, and as the speed increases, the world line of light approaches the time axis as shown in the graph above. This means that the speed of light is zero. There is a tragic situation where the speed of light becomes '0'.

The second is the collapse of invariants. As we have already mentioned, there are several invariants in relativity. However, when space-time becomes asymmetric, this invariant turns negative. This is not acceptable to anyone.



These two reasons are fatal. It will destroy the basic spirit of relativity symmetry and preservation. How can you say that time dilation - length contraction is a legitimate theory of relativity? If spacetime symmetry is not followed, there are some unacceptable things like this.


      1. The collapse of the constancy of the speed of light

      2. The collapse of a various invariants conservation quantity

      3. Lack of consistency in representation of time and length in the Minkowski spacetime diagram
      4. Impossible of developmental change of relativity
      5. The occurrence of many relativistic paradoxes

 For any situation involving length contractions, there is always a paradox. But if you interpret the paradox as an expansion of the length, it will be resolved too easily. Symmetry is precious. And it is even beautiful. It is simple and predictable. Are your choices symmetric or asymmetric? Which of the following two would you choose? Choice is free. (Sorry for the model.)

There is one more reason to choose length expansion rather than length contraction. Length contraction is not space-time symmetry, but length expansion is precisely space-time symmetry.


https://www.amazon.com/Length-Expansion-strengthened-relativity-theory/dp/8996138932/ref=sr_1_1?ie=UTF8&qid=1527045821&sr=8-1&keywords=length+expansion

Comments

Post a Comment

Popular posts from this blog

06 Muon Paradox

Image
   Today, I would like to talk about the muon paradox. There are several subatomic particles that are smaller than atoms, such as a μ-meson. It is called a μ-meson, but it is abbreviated to muon. The lifetime of this muon is fixed. The proper lifetime of this particle is 2.2 μsec. It only survives for a very short moment, and then  it collapses into other particles. Cosmic-rays are constantly coming out of space due to the explosion of stars in the universe or the nuclear fusion reaction of the sun. At this time, the cosmic-ray and the earth's atmosphere react to create a muon. Muon's speed is near the speed of light when it falls to Earth. It drops at a rate of about 0.998c. However, even if it falls so fast, it cannot reach the ground because its life is short. If the muon has a lifetime of 2.2 μ sec and a speed of 0.998 c, the muon can run about 650 m from the point where it was created. The point where the usual muon occurs is about 10km above sea le...
Read more

10 Rotating disc of black hole and Ehrenfest's paradox

Image
  Black holes are unusual in many ways. Thet have also has a spinning disc, a jet, a Schwartzchild radius, a horizon of events and singularities. But there is one thing that can not be explained in modern science or the theory of relativity. It is the rotating disc of a black hole. Black hole and Ehrenfest paradox   The speed at which materials rotate in the rotating disk of a black hole is almost as close as the speed of light. If so, all the materials must be decomposed and discarded by the Lorentz contraction. However, the rotating disk of a black hole certainly exists. It is definitely a contradiction. In fact, these are linked to the famous paradox of the Ehrenfest paradox. [1] Today, we will look at the Ehrenfest paradox. Fig. 1 Paul Ehrenfest Personally, I think Erlenpest paradox is the best of relativity's paradoxes. Other paradoxes seem to be a little simpler than this paradox. The list of people who studied this paradox is very extensive. Ein...
Read more

31. Ehrenfest Paradox 2: Does the length of a rotating circumference change?

Image
  We looked at the Ehrenfest paradox last time. There are two issues in the Ehrenfest paradox. The first assumes a disc made up of an ideal rigid body, but when rotated at relativistic speed, it ruptures. The second is that the perimeter of a rotating body is different from its length when it is stationary. In the last post I looked at the first issue, and this time I want to look at the second issue. For those who have not read the first part, I will briefly introduce this paradox. It is best to read the previous post. Below is a link to the first part. The Ehrenfest paradox part I Rotating disc and length contraction   In relativity, objects that run very fast are said to shrink in length. So the official name of this is Lorentz - Fitzgerald Length contraction. It is not 'Einstein's length contraction'. This was born regardless of the theory of relativity. Before the theory of relativity was published, several people experimented to detect ether, but the...
Read more