19. Relativistic circular wires paradox

Previously, when interpreting a straight wire as a theory of length contraction, we looked at some problems. Below is a link to my last post. Today we will look at the circular wire.

Origin of magnetic force

  It is well known that electric and magnetic forces are the same force. But it is still not easy to qualitatively understand it. Today's magnetic force is interpreted as the 'relativistic effect of moving charge'. This field was pioneered by Purcell. When I talked about the last straight wire, I had a little explanation, but let's take a look at it again.

Figure 1. Movement of charge from the lab point of view

The test charge moves to the speed of v to the right, and the negative charge moves to the speed of vo to the right. From the point of view of the test charge, it is as follows.

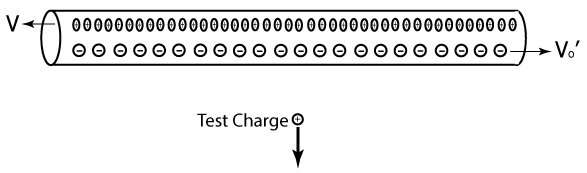Figure 2. The movement of charge from the viewpoint of the test charge

From the test charge's point of view, it is Purcell's calculations that the charge densities of the positive charge moving to the left at the speed of v and the negative charge moving to the right are changed as follows. So far it is justified. λ represents the charge density.

What we need to concentrate on here is a positive charge. The following is the formula for a positive charge only.

The expression of the charge density has the same form as the other expression of relativity theory, 'time dilation' or 'mass increase'.

   It is important to logically analyze the phenomenon of increasing charge density. For any natural phenomenon, there can be many ways to interpret it. Among the various theories, it is fundamental to explain the natural phenomena in question, and to be able to explain all previous experimental facts. And there should be no logical contradictions.

It is better to explain facts that have not been explained so far, or to predict and accurately predict unknown areas. At least you cannot predict an unknown field, but there should be no self-contradiction. This is a required condition.

The paradox of straight wires

   Let's briefly look at the problems of Purcell's interpretation. In common sense, if the charges only increased in speed from their place, it would have been as below. The number of electric charges per unit length of the conductor is the same, but the size of the positive electric charge is contracted.

Figure 5. Length contraction theory satisfying the law of charge conservation

From the point of view of the test charge, the charge density of the positive charge has been reduced, so it is necessary to generate the attraction force. But in reality, there is a repulsive force. Therefore, the interpretation shown in Figure 5 should be excluded from consideration.

Figure 6. Length contraction theory where charges converge to one side

As shown in Figure 6, if the positive charges are gathered in one direction due to the length contraction, one should have repulsive force along the wire and the other should have attraction. But this is totally different from real experiments or natural phenomena. This also cannot account for the actual nature and should be excluded from consideration. So, what can be explained by using length contraction? So what Purcell devised is as follows.

Figure 7. The official view of Purcell and the current relativity

This is the picture we first looked at. This results in a repulsive force on the test charge, which is consistent with the natural phenomenon. OK! Everything goes right in.

.

.

.

But if we explain this, we have new problems that we cannot think of. The number of positive charges per unit length of wire has increased. If so, is it against the law of conservation of charge? Of course, Purcell would have known this. So, Purcell assumed that when explaining this wire, it was infinitely long. Assuming an infinite wire, at least the problem of the number of charges will not arise. In fact, introducing infinity in science is often an excuse to avoid responsibility.

The paradox of the circular wires

For straight wire, Purcell assumes an infinite wire. Purcell has avoided contradictions by tightly arranging infinite charge. However, this is not possible for circular wire.  If a current flows through a circular wire, it is true that a magnetic force is generated. Clearly there is a natural phenomenon, so it is a good theory to be able to explain this well. The motif of this article is the site below. If you have any questions, please take a look around the site below.

     Magnetic Test of Length Contraction


Let's explain the magnetic phenomenon of a circular current by length contraction. How can we explain it? When there is no current in the wire, the different charges will be balanced and neutral as follows.

Figure 8. Non-relativistic circular wire

When the current flows, however, as the length contraction occurs as shown below: will the number of charges increase?  In the case of a straight wire, an infinite wire is assumed. Charges gathered and arranged tightly. So, we could explain the increase in charge density. However, in the case of a circular conductor, this assumption is impossible. In the figure above, the number of different charges is being balanced. However, in the figure below, the number of charges is not balanced. In other words, the violation of the law of conservation of charge is visible.

Figure 9. Purcell's circular wire

Therefore, nobody is trying to solve the problem of circular wire in this way. If this hypothesis is not correct, there are other ways as well. It is a way in which the charges protrude out of the wire, increasing the charge density. However, this method is not realistic. The reason is that the charge on the wire cannot flow out of the wire.

Figure 10. Alternative hypothesis of length contraction theory

So, what should we do now? In the case of straight wire, even if the law of conservation of charge is violated, it was possible to skip the problem assuming infinite wire. However, in the case of circular wire, even this is impossible. To solve this problem, we need an entirely new hypothesis for this situation. What hypothesis would you like to introduce? Or should we just leave it as a paradox?

Solving the circular wire paradox

"It is a paradox when it is interpreted as the theory of length contraction, but it becomes common sense when it is interpreted as the theory of length expansion."


   As always, if you think of length contraction, it is paradox, but if you think of length expansion, it makes sense. No long explanation is required. From the point of view of the test charge, the charge moving at the speed of v in the case of a circular wire will increase the charge density as follows.  The picture is as follows

Figure 11. Change in charge density of circular wires as claimed by the theory of length expansion

The expression is as follows.

It's just simple. The space representing the charge density has expanded as the length expands. All problems have been resolved cleanly. Therefore, considering the expansion of the length, there are several advantages below.

(1) Satisfies the law of conservation of charge quantity.
(2) Do not assume infinite wires.
(3) The increase in the charge density of the circular conductor can be explained.
(4) There is no need to introduce a new hypothesis to solve the paradox.


Your choice is yours.

Length Expansion(Amazon books)